Counting Regions in Images II
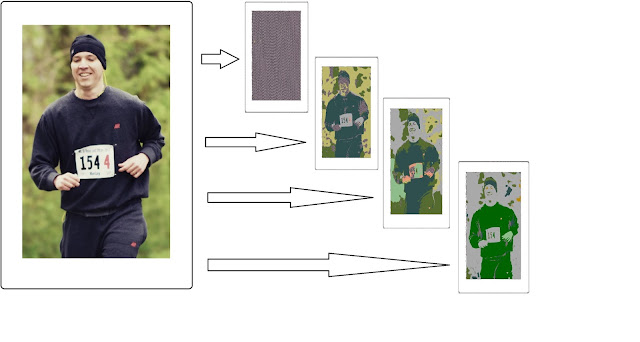
Carrying on from the previous post, in order to better illustrate the affects of the different thresholds, the thresholds were made as input parameters to this new algorithm, and in addition the color of each region was made different from each other, plus some bug fixes (casting fixes, etc.). To illustrate the concept I picked up an image of me running and applied the algorithm varying the thresholds. As you can see from the image below, the smaller the thresholds the more regions it finds, and conversely as we increase the thresholds the bigger and the fewer the regions are. If one makes the thresholds zero, it will imply that each pixel will be its own region. Similarly, when the threshold goes to infinity, the entire image becomes just one big region. Hope this helps - cheers, Boris. using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Drawing; using System.Collections; namespace CountRegi
