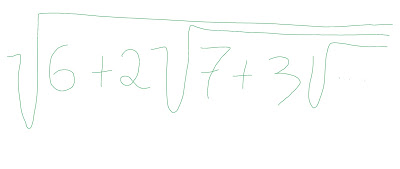Are there more strings than numbers?

Suppose (hypothetically) that you get this question during a round of technical/math interviews: "Create a 1-1 mapping between the natural numbers and every single conceivable string" Wow. Well, you may pull up your sleeves and start thinking about it. Start randomly: 0 -> "dog" 1 -> "cat" 2 -> "IDONTKNOW" 3 -> "Infinity" ... That's not a great strategy. Clearly you need some order on the right side of the mapping. But if we think about order, you may end up in a situation where you'll convince yourself that there are way more strings than natural numbers . Without loss of generalization, we'll assume only strings in the alphabet of the uppercase English letters. Suppose that you start mapping each number to a sequence of "A"s. Take a look at image below: With this approach we have exhausted all the natural numbers (notice the Googleplex there) without even getting to reach the l