Prefix Sum: Trading Space for Time
This problem can be solved with a Prefix Sum approach. Basically we can calculate and store the partial array sum from 0..i, for each i. That way we can easily compute the average needed (just use long for the prefix sum array since the addition may go past Max.Int). This way we're trading space (O(n)) for time (also O(n)). Code is down below, cheers, ACC.
2090. K Radius Subarray Averages
Medium
You are given a 0-indexed array nums of n integers, and an integer k.
The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.
Build and return an array avgs of length n where avgs[i] is the k-radius average for the subarray centered at index i.
The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.
- For example, the average of four elements
2,3,1, and5is(2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to2.
Example 1:

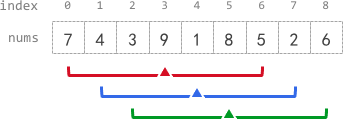
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3 Output: [-1,-1,-1,5,4,4,-1,-1,-1] Explanation: - avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index. - The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37. Using integer division, avg[3] = 37 / 7 = 5. - For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4. - For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4. - avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.
Example 2:
Input: nums = [100000], k = 0 Output: [100000] Explanation: - The sum of the subarray centered at index 0 with radius 0 is: 100000. avg[0] = 100000 / 1 = 100000.
Example 3:
Input: nums = [8], k = 100000 Output: [-1] Explanation: - avg[0] is -1 because there are less than k elements before and after index 0.
Constraints:
n == nums.length1 <= n <= 1050 <= nums[i], k <= 105
Accepted
7,404
Submissions
19,468
public int[] GetAverages(int[] nums, int k)
{
long[] prefixSum = new long[nums.Length];
prefixSum[0] = nums[0];
for (int i = 1; i < nums.Length; i++)
{
prefixSum[i] = nums[i] + prefixSum[i - 1];
}
int[] retVal = new int[nums.Length];
for (int i = 0; i < retVal.Length; i++)
{
if (i - k >= 0 && i + k < retVal.Length)
{
retVal[i] = (int)((prefixSum[i + k] - prefixSum[i - k] + nums[i - k]) / (2 * k + 1));
}
else
{
retVal[i] = -1;
}
}
return retVal;
}
Comments
Post a Comment